KI: Unterschied zwischen den Versionen
Vogty (Diskussion | Beiträge) graphviz Bilder ersetzt |
|||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{review}} | {{review}} | ||
== Endliche Automaten == | == Einfaches Verhalten durch Endliche Automaten == | ||
Eine einfache Möglichkeit in einem Computerspiel eine nicht vom Spieler gesteuerte Einheit mit 'Intelligenz' auszustatten führt über [http://de.wikipedia.org/wiki/Endlicher_Automat Endliche Automaten (FSM)]. Hierbei werden verschiedene Zustände definiert und Bedingungen für Übergänge zwischen diesen Zuständen. | Eine einfache Möglichkeit in einem Computerspiel eine nicht vom Spieler gesteuerte Einheit mit 'Intelligenz' auszustatten führt über [http://de.wikipedia.org/wiki/Endlicher_Automat Endliche Automaten (FSM)]. Hierbei werden verschiedene Zustände definiert und Bedingungen für Übergänge zwischen diesen Zuständen. | ||
Ein einfaches Beispiel wäre ein Monster, dass solange patrouilliert bis ein Spieler zu nahe kommt und anschliessend in den Angriff übergeht. Sollte der Spieler zuviel Schaden anrichten soll es dann fliehen. Hierfür wären folgende Zustände und Übergänge nötig: | Ein einfaches Beispiel wäre ein Monster, dass solange patrouilliert bis ein Spieler zu nahe kommt und anschliessend in den Angriff übergeht. Sollte der Spieler zuviel Schaden anrichten soll es dann fliehen. Hierfür wären folgende Zustände und Übergänge nötig: | ||
| Zeile 28: | Zeile 28: | ||
Der zugehörige Endliche Automat würde folgendermassen aussehen: | Der zugehörige Endliche Automat würde folgendermassen aussehen: | ||
<center> | <center> | ||
[[Datei:KI FSM.png]] | |||
<!-- | |||
<graphviz> | <graphviz> | ||
digraph FSMMonster { | digraph FSMMonster { | ||
| Zeile 42: | Zeile 45: | ||
} | } | ||
</graphviz> | </graphviz> | ||
--> | |||
</center> | </center> | ||
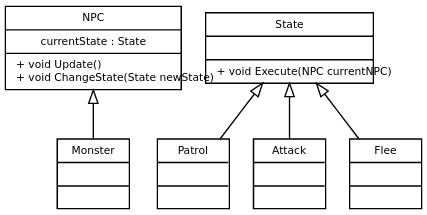
Es gibt viele Architekturen für Endliche Automaten, im Folgenden wird ein [[Objektorientierung|objektorientierter]] Ansatz aufgezeigt der leicht umsetzbar und flexibel ist. | Es gibt viele Architekturen für Endliche Automaten, im Folgenden wird ein [[Objektorientierung|objektorientierter]] Ansatz aufgezeigt der leicht umsetzbar und flexibel ist. | ||
<center> | <center> | ||
<graphviz> | [[Datei:KI Vererbung.png]] | ||
<!--<graphviz> | |||
digraph Vererbung { | digraph Vererbung { | ||
rankdir = BT | rankdir = BT | ||
| Zeile 93: | Zeile 98: | ||
} | } | ||
</graphviz> | </graphviz> | ||
--> | |||
</center> | </center> | ||
Aktuelle Version vom 22. Oktober 2020, 08:56 Uhr
Einfaches Verhalten durch Endliche Automaten
Eine einfache Möglichkeit in einem Computerspiel eine nicht vom Spieler gesteuerte Einheit mit 'Intelligenz' auszustatten führt über Endliche Automaten (FSM). Hierbei werden verschiedene Zustände definiert und Bedingungen für Übergänge zwischen diesen Zuständen. Ein einfaches Beispiel wäre ein Monster, dass solange patrouilliert bis ein Spieler zu nahe kommt und anschliessend in den Angriff übergeht. Sollte der Spieler zuviel Schaden anrichten soll es dann fliehen. Hierfür wären folgende Zustände und Übergänge nötig:
| Zustand | Bedingung | Folgezustand |
|---|---|---|
| Patrol | PlayerIsNear | Attack |
| Attack | OwnHealth < 25 | Flee |
| Attack | PlayerIsDead | Patrol |
| Flee | NOT PlayerIsNear | Patrol |
Der zugehörige Endliche Automat würde folgendermassen aussehen:
Es gibt viele Architekturen für Endliche Automaten, im Folgenden wird ein objektorientierter Ansatz aufgezeigt der leicht umsetzbar und flexibel ist.
Die Idee die in diesem UML Klassendiagramm dargestellt wird macht es möglich das Verhalten vollständig von der restlichen Implementierung der NPCs[1] zu trennen. Ein Monster würde sich also zu jedem Zeitpunkt in einem der drei Zustände befinden und beim Aufruf von Update() die Execute() Methode des Zustandes aufrufen in dem es sich befindet. Die Implementierung der einzelnen Zustände kann nun wiederum in der Execute() Methode die Bedingungen zur Transition überprüfen und gegebenenfalls durch aufrufen von ChangeState() einen Übergang auslösen.
Pathfinding
Beim Pathfinding geht es darum Spielobjekte möglichst geschickt durch die Spielwelt zu bewegen und dabei statischen Hindernissen und anderen Spielobjekten auszuweichen. Ein gutes Pathfinding, das in allen Situationen nachvollziehbares Verhalten produziert ist eine anspruchsvolle Aufgabe. Im folgenden werden die Grundlagen Schritt für Schritt erläutert.
Auf einen Punkt zubewegen
Als Grundlage aller Wegfindungsalgorithmen muss erst einmal gewährleistet sein, dass ein Spielobjekt gezielt auf einen definierten Punkt in der Spielwelt bewegt werden kann.
Einfache Bewegung
Hier wird davon ausgegangen, dass die Spielobjekte über Koordinaten verfügen, die mehr oder weniger direkt manipuliert werden. D.h. die Aufgabe besteht hier darin, in jedem Zeitschritt aus den alten Koordinaten und der Geschwindigkeit des fraglichen Spielobjektes die neuen Koordinaten zu berechnen.
- Berechnen des Richtungsvektor vom Spielobjekt zum Zielpunkt
- Normalisieren des Richtungsvektors
- Skalieren des Richtungsvektors in Abhängigkeit von der Geschwindigkeit des Spielobjektes
- Der erhaltene Vektor wird auf die aktuellen Koordinaten des zu bewegenden Spielobjektes aufaddiert
Ist die Zielposition mit ausreichender Genauigkeit erreicht, so wird keine weitere Bewegung mehr durchgeführt. Zu beachten ist hierbei, dass bei zu grossen Geschwindigkeiten das Spielobjekt über das Ziel hinausschiessen kann. Um dies zu verhindern kann die Geschwindigkeit zusätzlich von Abstand zum Ziel abhängig gemacht werden. Falls das Spielobjekt dem Ziel also schon sehr nahe ist, wird die Bewegungsgeschwindigkeit verringert.
Steering
Bei Objekten die nicht direkt, sondern durch Krafteinwirkung, gesteuert werden, z.B. Autos, Raumschiffe oder ähnliches, ist die Bewegung etwas anspruchsvoller. Es wird hier von einem vereinfachten Prinzip ausgegangen, welches eine Krafteinwirkung von der Seite zur Richtungssteuerung des Spielobjektes vorsieht. Die Vorwärtsbewegung wird ebenfalls durch Krafteinwirkung von hinten realisiert.
- Berechnen des Richtungsvektor vom Spielobjekt zum Zielpunkt
- Falls die Ausrichtung des Spielobjekts Links vom berechneten Richtungsvektor liegt -> Krafteinwirkung von Links
- Falls die Ausrichtung des Spielobjekts Rechts vom berechneten Richtungsvektor liegt -> Krafteinwirkung von Rechts
Auch hier gilt es darauf zu achten, dass bei Erreichen der Zielposition der Vorwärtsschub verringert bzw. abgestellt wird.
Graphen generieren
Viele Wegfindungsalgorithmen verwenden Graphen als unterliegende Datenstruktur um optimale Wege zum Ziel planen zu können. Die Knoten eines solchen Graphe sollten erreichbare Wegpunkte sein und die Kanten repräsentieren begehbare Wege innerhalb der Spielwelt. Es gibt mehrere Möglichkeiten einen solchen Graphen aufzuspannen.
- Manuelles platzieren der Knotenpunkte und Kanten
- Programmatische Aufteilung der Spieltwelt
Pfad berechnen
- A*
- ↑ Non Player Character, dt.: Nicht Spieler Charakter, alle Figuren die nicht vom Spieler sondern vom Computer gesteuert werden