QuadTree/Einleitung: Unterschied zwischen den Versionen
Aus Das Sopra Wiki
Justus (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Justus (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Ein QuadTree<ref>[[wikipedia:de:Quadtree|Wikipedia Artikel]] zu QuadTrees</ref> ist eine Datenstruktur mit der eine 2-Dimensionale Welt repräsentiert werden kann. Die Welt wird dazu in vier gleich große Rechtecke eingeteilt. Damit man viele Objekte effizient organisieren kann wird nur eine bestimmte Anzahl ''n'' Objekte in einer Zalle (Quad) gespeichert. Falls die gespeicherte Anzahl der Objekte ''n'' übersteigt wird das betroffene Quad in vier neue Quads geteilt und die vorhandenen Objekte auf die vier neuen Quads verteilt. | Ein QuadTree<ref>[[wikipedia:de:Quadtree|Wikipedia Artikel]] zu QuadTrees</ref> ist eine Datenstruktur mit der eine 2-Dimensionale Welt repräsentiert werden kann. Die Welt wird dazu in vier gleich große Rechtecke eingeteilt. Damit man viele Objekte effizient organisieren kann wird nur eine bestimmte Anzahl ''n'' Objekte in einer Zalle (Quad) gespeichert. Falls die gespeicherte Anzahl der Objekte ''n'' übersteigt wird das betroffene Quad in vier neue Quads geteilt und die vorhandenen Objekte auf die vier neuen Quads verteilt. | ||
Im folgenden Beispiel wird angenommen, daß ''n''=<tt> | Im folgenden Beispiel wird angenommen, daß ''n''=<tt>4</tt> | ||
[[Bild:QuadTeilen.png|none|Quad teilen]] | [[Bild:QuadTeilen.png|none|Quad teilen]] | ||
Version vom 23. April 2009, 17:43 Uhr
Ein QuadTree[1] ist eine Datenstruktur mit der eine 2-Dimensionale Welt repräsentiert werden kann. Die Welt wird dazu in vier gleich große Rechtecke eingeteilt. Damit man viele Objekte effizient organisieren kann wird nur eine bestimmte Anzahl n Objekte in einer Zalle (Quad) gespeichert. Falls die gespeicherte Anzahl der Objekte n übersteigt wird das betroffene Quad in vier neue Quads geteilt und die vorhandenen Objekte auf die vier neuen Quads verteilt.
Im folgenden Beispiel wird angenommen, daß n=4
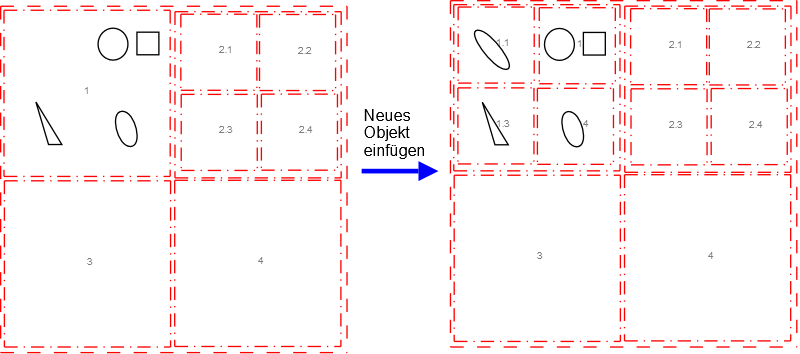
Dabei entsteht ein Baum, der in etwa so aussehen könnte:
<graphviz> digraph B {
Wurzel -> 1;
Wurzel -> 2;
Wurzel -> 3;
Wurzel -> 4;
2 -> 2.1;
2 -> 2.2;
2 -> 2.3;
2 -> 2.4;
} </graphviz>
- ↑ Wikipedia Artikel zu QuadTrees
